300ぶんの1なのに100回転で当たった!
逆に1000回転ハマった!
なんで大当たりはこんなに
当たったり当たらなかったり「バラバラ」になるの?
実は大当たりはバラバラに見えて
「発生しやすいゾーン」が決まっています。
- 大当たりの発生確率とは?
- 発生しやすいゾーンとは?
- 発生確率を知るメリットとは?
これらの内容が分かりますので、ぜひ参考にしてください!
【関連動画】
記事と同様の内容が動画でも見られます。
取り組みやすい方をお選びください。
【結論】大当たりは「中央値以下」が発生しやすい
先に結論をまとめるとーーー
大当たりは「中央値以下」が発生しやすいです。


300分の1であれば中央値は「約200」
200分の1であれば「約140」
そして発生確率を知るメリットは
- 立ち回りの参考にできる
- ストレスを減らせる
こうしたメリットがあります
 保全士:ひろのぶ
保全士:ひろのぶ今回はこの中央値を含めた「発生確率」をメインに解説していきます!



パチンコ・スロットの基本といえば基本ですので、勝ちたい人もやめたい人も楽しみたい人も役に立つと思います!
【説明1】大当たりの確率とは何か
パチンコにおける「大当たり確率」は
1回転ごとに「抽選される確率」です。
スロットであれば設定された
「当選フラグが成立する確率」で
まぁ似たようなものです。
よく見聞きする言い方は300ぶんの1ですが
パーセントのほうが分かりやすいのかなと思うので
言い換えるとこのようになります。
| 項目 | 言い換え | 補足 |
| 分数 | 1/300 | 最も基本的な表。 |
| 小数 | 0.00333 | 1を300で割った値 |
| パーセント | 0.33% | 100をかけた割合 |
ですので300ぶんの1であればーーー
1回転につき「0.33%で大当たり」
そしてこの抽選は「毎回独立」しています。
100回転だろうが、1000回転だろうが
「大当たりの確率は0.33%で一定」です。
この確率の抽選が
「無限にどこまでも続く」のがパチンコです。



ちなみに例外として
スロットのように「天井があれば有限」になります。
【説明2】発生確率とは?
「大当たりの確率は一定」なのですが
それでも「発生しやすいゾーン」というものが存在します。
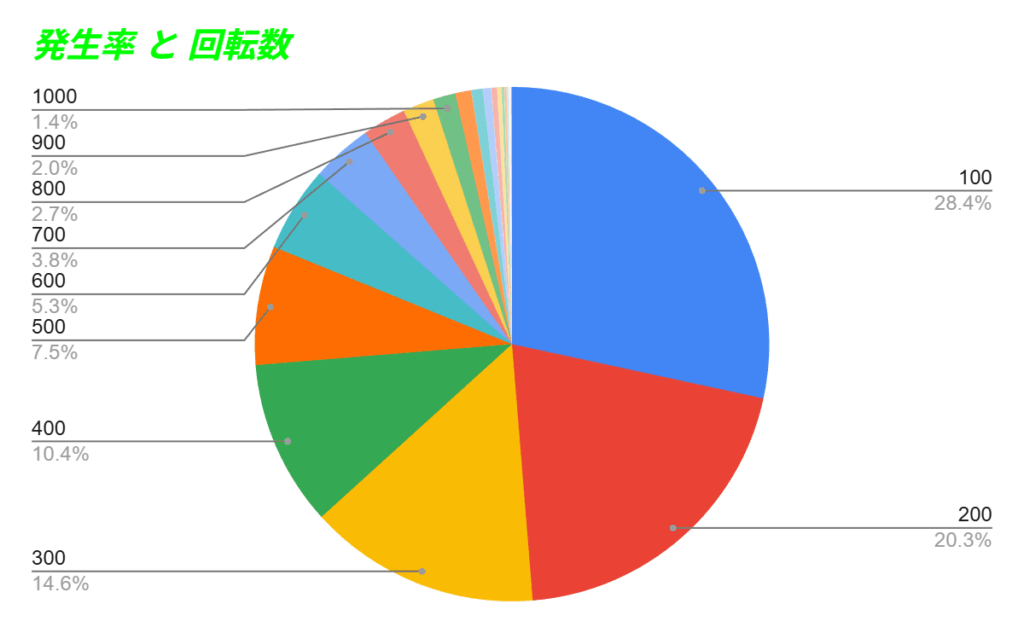

これは300ぶんの1の大当たり「発生確率のグラフ」です。
右上の100というのは
大当たり「100回転以内が28.4%を占める」
という意味です。
つまり300ぶんの1の遊技台であれば
- 100回転以内に約30%の確率で大当たり
- 100から200回転以内なら約20%で大当たり
こうした「発生確率」が決まっています。
【説明3】中央値とは?
そしてこれらを足していって
キリの良い数値である「50%」の部分が約200回転で
これが「中央値」になります


この中央値は言い換えると
大当たりの「半分は中央値以内で発生する」ということで
文字通り「大半がここに収まります」
ですので中央値以内が「発生しやすいゾーン」になります。
【補足1】分母の回転数発生確率は?
50%を超えてみていくと、300ぶんの1の分母と同じ300回転は
「発生確率の累計63.3%」になります


これは知っている人も多いでしょうが
100ぶんの1が100回以内に当たる確率。
これは63.3%です。
これと同じで100だろうが300だろうが500だろうが
数値がでかくなっても
「分母と同じ回転数までの確率は一緒」です
【補足2】発生確率の累計
ちなみに計算内容としては
先ほどの「1回転につき0.33%で大当たり」
ここから計算できます。


| 回転数(回) | 到達確率 (%) | 発生率 (%) | 発生累計 (%) |
|---|---|---|---|
| 1 | 100.00 | 0.33 | 0.33 |
| 2 | 99.67 | 0.33 | 0.67 |
| 3 | 99.33 | 0.33 | 1.00 |
| 4 | 99.00 | 0.33 | 1.33 |
| 5 | 98.67 | 0.33 | 1.66 |
| 6 | 98.34 | 0.33 | 1.98 |
| 7 | 98.02 | 0.33 | 2.31 |
| 8 | 97.69 | 0.33 | 2.64 |
| 9 | 97.36 | 0.32 | 2.96 |
| 10 | 97.04 | 0.32 | 3.28 |
こんな感じで「到達できる確率」を割り出すことができます。
1回転目は100%
2回転目は99.67%
この時、回転数に対する「発生確率は徐々に下がって」いきます。
これは、もし1回転目で当たっていたら2回目に到達できないからです。
その徐々に下がっていく「発生確率」、その「累計の数値」。
この累計の数値が「その回数以下の発生確率」になります。



今回の場合
10回以内は3.28%で発生する確率ですね。
【注意点】確率は変わっていない
ここでややこしいのが
大当たりの「確率が変わっている」わけではないということ。
冒頭で「発生しやすいゾーン」と言いましたが
これは「当たりやすいゾーン」とは意味が違います。
単純に「チャンスが多い場所」が「発生確率が高くなる」
そしてもっともチャンスが多い場所、それは「1回転目」。
ですが特別1回転目が優れているといった意味ではないです。
【説明4】なんのメリットがあるの?
じゃあこの発生確率って
知ることで「何のメリットがあるのか」
それは「ストレス」や「判断ミス」を減少させることができます。
取説になる
まずこの発生確率といった「計算上起こりえる数値」というのは
一種の「取説みたいなもの」です。
そして私たちが実際に打って「体験しやすい」
もしくはスランプグラフなど「目にしやすい」のは
今回の「発生しやすいゾーン」での大当たりになります。
なんといっても発生確率50%ですからね。
取説無し
これを「取説」もなく体験してしまうと
- なんでこんなに当たらないのか
- 逆になんで意外とあっさり当たるのか
こうした「なんで?」という疑問が全部
「分からないまま終わってしまう」
そして疑問は次第に苛立ちに変わり
「ストレス」になったり
この台は悪いとそれほど悪くなかったのに
「判断ミス」をして負けに繋がります
取説有り
逆に「取説」をもっておけば
- こんなに当たらないのは「10%」だからあり得る確率。
- あっさり当たったのは「30%」を引けたから
- 台が悪いと思ったけどこれで大体「50%」だった
こんな感じで「疑問の答え」が分かります。
【補足3】
発生確率のグラフから分かること
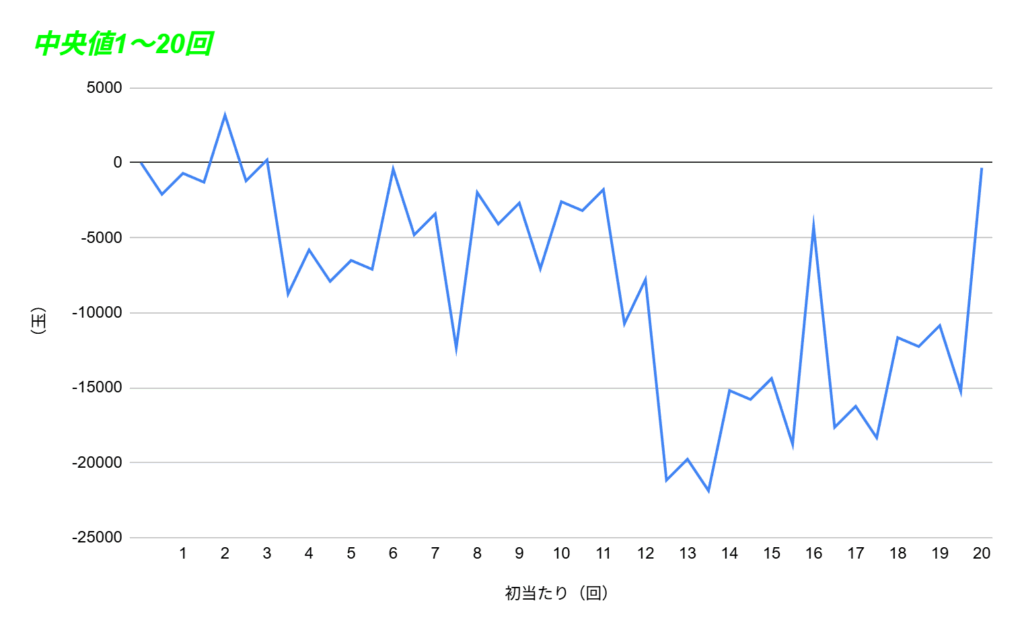

他にもこの中央値や発生確率から
「現実的に起こりえる出玉のグラフ」を作成できます。
こうして発生確率から計算してグラフにすると
平均値だけでは分かりにくい浮き沈みが
「当然のように発生する」ということが分かります。
このグラフに関しては別の記事で解説していますので、詳しく知りたい方はそちらをぜひ見てみてください!
【補足4】
中央値を基準に判断する
他にも中央値を基準にどれくらい運がよかった、悪かったが判断できたりします
| 連続回数 (n) | 確率(パーセント) | 分数(何分の1) |
|---|---|---|
| 1回 | 50.00% | 2分の1 |
| 2回 | 25.00% | 4分の1 |
| 3回 | 12.50% | 8分の1 |
| 4回 | 6.25% | 16分の1 |
| 5回 | 3.13% | 32分の1 |
| 6回 | 1.56% | 64分の1 |
| 7回 | 0.78% | 128分の1 |
| 8回 | 0.39% | 256分の1 |
| 9回 | 0.20% | 512分の1 |
| 10回 | 0.10% | 1,024分の1 |
これはコインの裏表と同じで、50%が連続して発生する確率です
中央値50%を基準に考えることで
5連続で発生した!意外とあり得る確率だ
などが判断できたりします。
【まとめ】発生確率は取説になる
今回の内容から分かるように
実は「発生確率」を見ると
大当たりは「バラバラ」に見えて
「発生しやすいゾーン」が決まっています。



ですので
「勝ちたいひと」にも
「楽しみたいひと」にも
「やめたいひと」にも



この「発生確率」という
「取説」が役に立つと思います
備考
関連記事
このサイトが大切にしていること
「この世界は、生きづらいものだ」と思っていた過去があります。
でも今は、そう感じていたのは“思考の回路”が乱れていただけだったんだと気づきました。
このサイト「ゆるやめ」では機械保全士として培った現実重視の“視点”をベースに、脳科学や心理学の知識そして私自身の体験を交えて、我慢ではなく緩やかな仕組みでやめるヒントをお届けしています。
よければ他の記事も覗いてみてくださいね。








