パチンコ「eルパン三世VSキャッツ・アイ」では、大体こんな展開になる。計算してみた!
「スペック」や「出玉に関する数値」が分かりますので、ぜひ参考にしてください。
【関連動画】
記事と同様の内容が動画でも見られます。取り組みやすい方をお選びください。
【結論】大体こんな展開になる
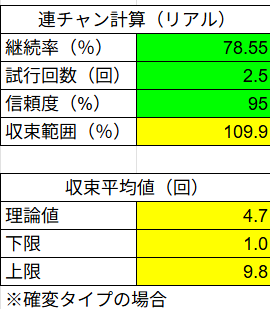
多くの場合、このグラフのような展開になります。
グラフ&数値

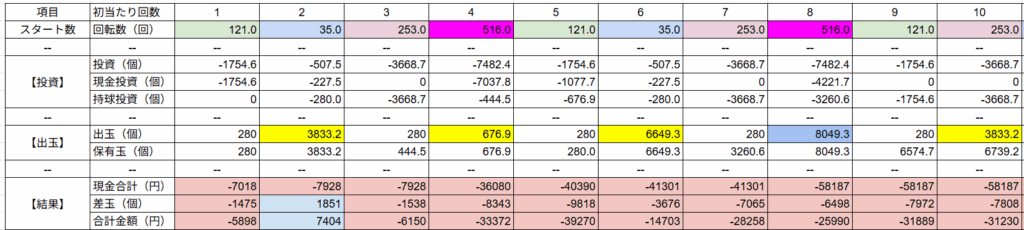
大当たりは121回転や35回転といった浅い当たりや、253回転のほぼ平均の当たり。
そして516回転といった少し深いハマリが発生。
出玉は通常が300個で、ラッシュでは3500個や6500個。
少し多めの8000個といった出玉が発生します。
ですがトータルとしては平均値以下となり、差玉で言えばマイナス7800個。
交換率など考慮するとマイナス31,000円。
必要軍資金は初当たり10回で「約58,000円」となりました。
ここからは、なぜこうなるのかを話していきます。
【説明1】スペック紹介
まずスペックの解説をします。
スペック
| 項目 | 数値 | ロス有 | 補足 |
|---|---|---|---|
| 大当たり確率(回) | 257.9 | — | |
| ラッシュ突入確率(%) | 50.00 | — | |
| ラッシュ突入必要平均回数(回) | 2.00 | — | |
| ラッシュ継続率(%) | 78.55 | — | |
| 平均継続回数(回) | 3.661 | — | STタイプ |
| ラッシュ平均期待値(個) | 7413.7 | 6919.5 | 1R当たりチェッカー回数分マイナス |
| ラッシュ平均期待値+初当たり(個) | 7713.7 | 7199.5 | ↑ |
| トータル初当たり期待値(個) | 4006.8 | 3739.7 | ↑ |
※数値はネット参考+独自計算の結果
初当たり
初当たりで、大当たりの確率は257分の1。
ラッシュ突入確率は約50%で、時短はありません。
| 項目 | % | 出玉 | 出玉(ロス有) | ラウンド数 | モード移行 |
|---|---|---|---|---|---|
| 割合 | 50.0 | 300 | 280 | 2 | 通常へ |
| 50.0 | 300 | 280 | 2 | ラッシュへ |
ラッシュ中
無事ラッシュ突入した場合で、
| ST継続率 | 値 |
|---|---|
| 当たり確率 | 99.9 |
| ST回数 | 153 |
| 継続率 | 78.55 |
| 平均継続回数 | 3.66 |
ラッシュはSTタイプ。
性能は大当たり確率約99分の1、ST回数153回ですので、「継続率は約78.5%」。
平均継続回数は「約3.6回」になります。
ラッシュ中ボーナス割合
ラッシュ中のボーナスの割合で、
| 項目 | % | 出玉 | 出玉(ロス有) | ラウンド数 | モード移行 |
|---|---|---|---|---|---|
| 割合 | 15.00 | 0 | 0 | 0 | ラッシュへ |
| 35.00 | 1500 | 1400 | 10 | ラッシュへ | |
| 50.00 | 3000 | 2800 | 20 | ラッシュへ |
「約15%が0個でST回数回復のみ」
「約35%が1500個」
「約50%が3000個」
「約15%」が実質出玉無しのため、平均継続回数「約3.6回」ですが、出玉ありで考えると「約3.0回」。
| 平均出玉 | 平均出玉(ロス有) | ラウンド数 |
|---|---|---|
| 2025.00 | 1890.00 | 13.5 |
この出玉無しも含めて、ラッシュ中のボーナス単体での大当たり平均期待値は、1回当たり約2000個になります。
ラッシュ1回の期待値
そしてラッシュ全体の期待値で考えると、先ほどの約2000個が約3.6回で、「約7400個」になります。
| 平均出玉 | 平均出玉(ロス有) | ラウンド数 | 平均継続回数 |
|---|---|---|---|
| 7413.7 | 6919.5 | 49.4 | 3.661 |
スペックまとめ
| 項目 | 値 |
|---|---|
| ラッシュ期待値 | 7413.7 |
| 初当たり+ラッシュ | 7713.7 |
| 初当たり+ラッシュ(ロス有) | 7199.5 |
| トータル初当たり期待値 | 4006.8 |
| トータル期待値(ロス有) | 3739.7 |
| 出玉ロス | 267.1 |
| ラウンド数 | 26.7 |
| 1R確率 | 9.7 |
| ボーダー(4.0円) | 17.2 |
ここまでの数値を整理すると、
ラッシュ期待値は約7400個で、初当たりを含めた場合、約7700個。
アタッカーの出玉ロスを考慮すると約7200個。
トータル初当たり期待値は約3700個。
そして等価の場合はボーダーが約17.2回転。
このようなスペックになります。
 保全士:ひろのぶ
保全士:ひろのぶ「eルパン三世VSキャッツ・アイ」では初当たりは軽めだけど300個。時短もないので通常を引くと厳しい展開になる。そしてラッシュでも実質平均3連なので、思ったより出にくそうな印象です。
【説明2】リアルの平均値は「発生率」で変わる
ここからはこのスペックで、なぜ冒頭のグラフのようになるのかを話ていきます。
まず注意点で、計算上ボーダーの数値で遊技していれば最終的に差玉はほぼ0になります。
ただリアルでは「発生率」が影響して「平均値」が大きく変わります。
大当たり回転数「発生率」
まずは大当たり回転数で、このグラフは次の数値で作られています。


| 初当たり回転数 | |
|---|---|
| 大当たり確率 | 257.9 |
| 発生累計(25%) | 75 |
| 中央値(50%) | 179 |
| 発生累計(75%) | 357 |
| 発生累計(90%) | 593 |
| 発生累計95%) | 772 |
この数値は、大当たりが発生する回転数の割合を計算した、発生確率の累計です。
今回の場合は大当たり「179回転以内」が50%で発生。
75%まで考慮した場合なら「357回転」。
90%なら「593回転」です。
このグラフでは0から25%の間の数値、25から50%の間の数値といった感じで、90%以内の数値を抜粋して割り振っています。
ちなみにこの発生確率50%は中央値と呼ばれ、その数値以内が全体の50%を占める回数、真ん中の値のことです。
ちなみに100回転ごとの発生率ではこのようになります。
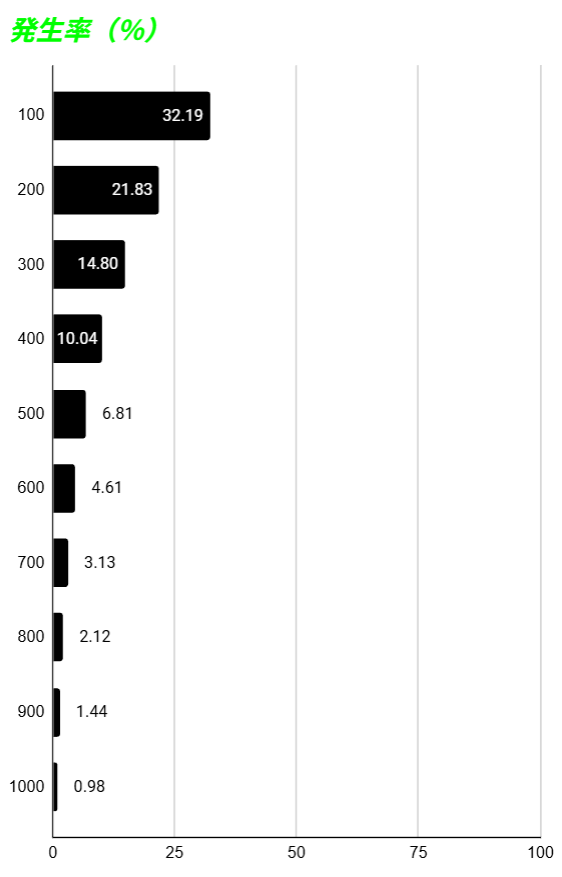

100回転以内が「約32%」、100から200回転以内が「約21%」と、かなりの割合を占めています。
ラッシュ継続回数「発生率」
| ラッシュ継続率 | |
|---|---|
| 継続率 (%) | 78.55 |
| 平均回数 | 3.661 |
| 発生累計(25%) | 0.21 |
| 中央値(50%) | 1.88 |
| 発生累計(75%) | 4.76 |
| 発生累計(90%) | 8.56 |
| 発生累計(95%) | 11.43 |
次はラッシュ平均継続回数で、これも先ほどと同様、発生確率から数値を抜粋しています。
継続回数「1.8回以内」が50%で発生。
75%まで考慮した場合なら「4.7回」。
90%なら「8.5回」です。
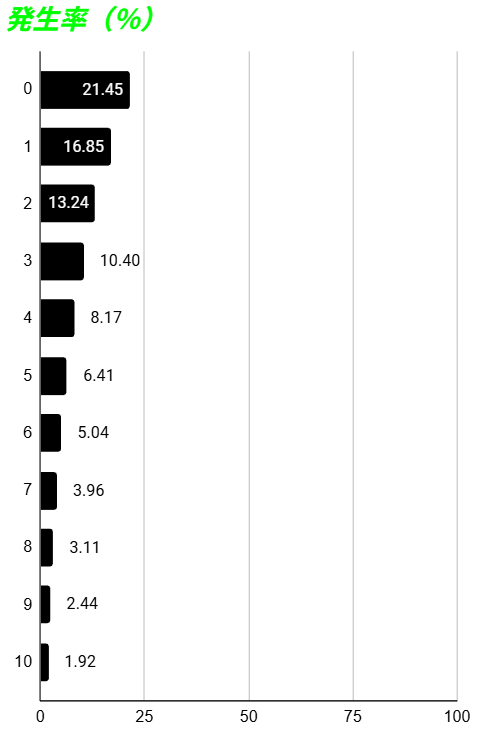

1回ごとの発生率ではこのようになります。
0回が「約21%」、1回が「約16%」と、かなりの割合を占めています。
発生率の影響
今回のグラフは、こうした発生率が高い90%以内の数値を抜粋して割り振ることで、リアルに近づけています。
そしてこれらの数値の平均を計算すると、
- 大当たり回転数:平均「約257回」は「約222回」
- ラッシュ継続回数:平均「約3.6回」は「約2.3回」
- トータル初当たり期待値:平均「約3700個」は「約2400個」
このような数値になり、「当たりやすく」、「伸びにくく」、「トータル出にくく」なります。
【説明3】平均値になる流れ
さきほどのグラフからどんどん回数を重ねると平均値に近づきます。
グラフ&数値
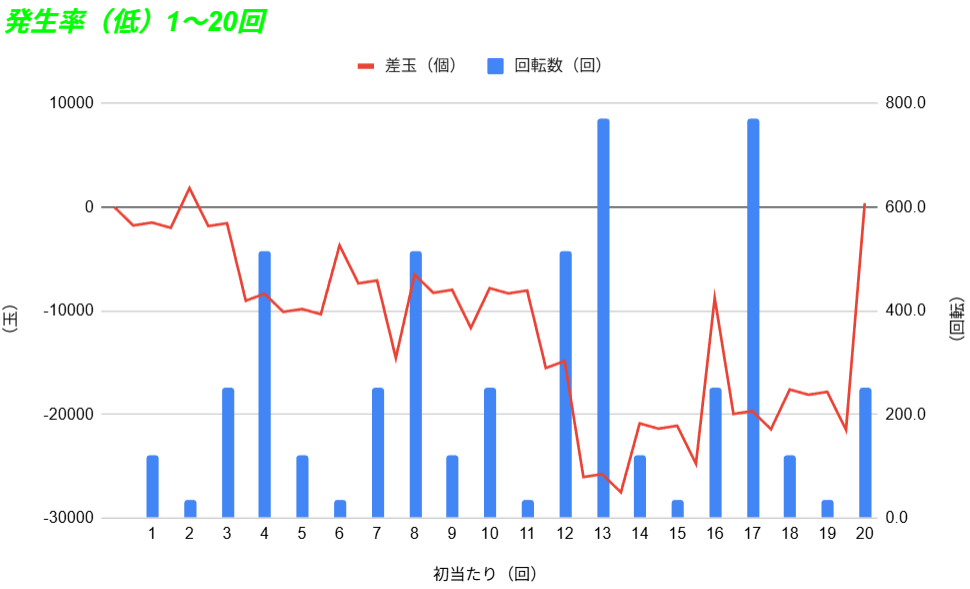

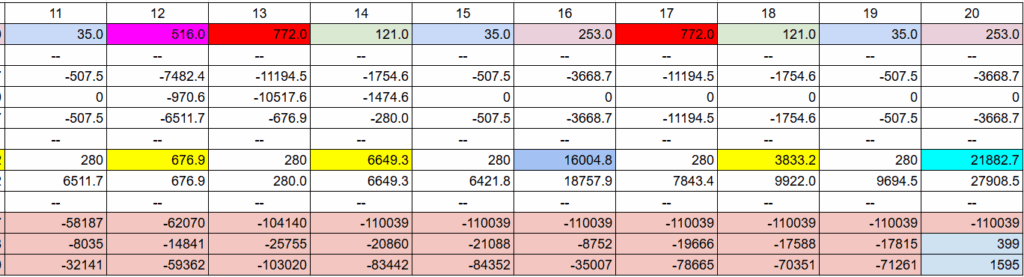

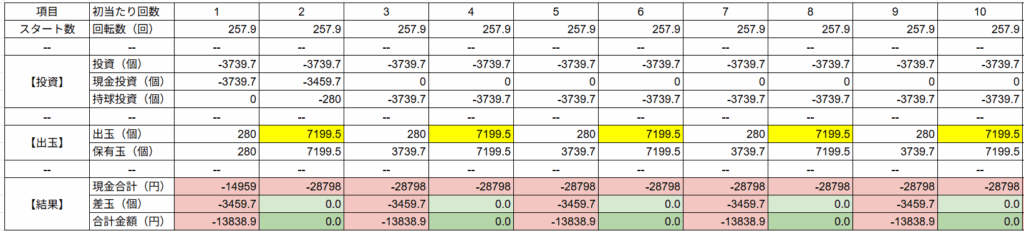
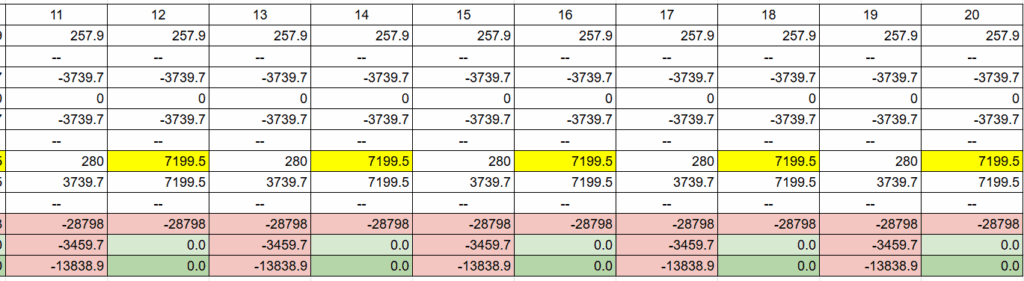
このグラフは「前半」の1から10回が、先ほどまでの90%、「発生率が高い展開」です。
「後半」の11から20回が、残り10%の数値を組み込んだ、「発生率が低いレアな展開」です。
大当たりは先ほどと同じ121回転や35回転といった浅い当たりや、253回転のほぼ平均の当たり。
516回転といった少し深いハマリ。
そしてさらにレアな772回転といった大ハマりが発生。
出玉は通常が300個で、ラッシュでは3500個や5000個。
少し多めの16000個といった連チャン。
そしてさらにレアな21000個といった大連チャンが発生。
こうして10%の「発生率が低いレアな展開」を引くことで平均値になっていきます。
| レート | 項目 | 平均 | 1~10回 | 1~20回 |
|---|---|---|---|---|
| 【交換率】 | 232玉貸し出し | -31029.6 | -62697.0 | -118566.8 |
| 27玉交換(3.70円) | 26638.0 | 24935.2 | 103261.4 | |
| 金額 | -4391.7 | -37761.8 | -15305.4 |
最終的にトータルとしては差玉で言えばほぼ0個。
交換率など考慮するとマイナス15,000円。
必要軍資金は初当たり20回で「約120,000円」となりました。
ちなみに、引きたくない10%のレアな大ハマりは、大連チャンより多く発生します。
単純に初当たりとラッシュで頻度が違うからで、今回であればラッシュは約50%。
ですので大ハマり2回,大連チャン1回といった感じです。
言い換えると大連チャンは、初当たり20回に1回程度発生します。
【補足】平均値への収束&ボーダー
補足として、平均値への収束とボーダーについて話していきます。
平均値への収束
平均値への収束ですが、今回は分かりやすくするために前半、後半と展開を分けて、平均になるようにしました。
でも実際には何十万回転と経て平均値になります。
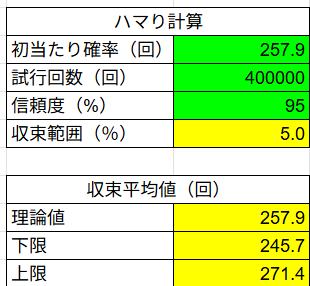

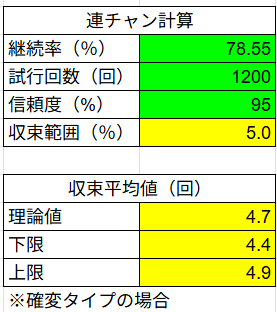

計算上今回の場合では
- 大当たり回数はスタート回数約「40万回転」で収束。
- ラッシュ継続回数はラッシュ突入回数約「1200回」で収束。
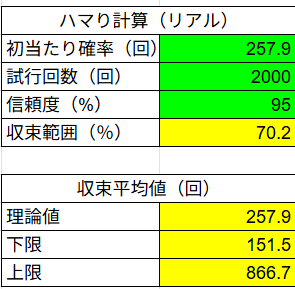


1日の場合は大体次の感じになり
- 大当たり回数はスタート回数約「2,000」の場合、下限151回、上限866回が平均になりえる。
- ラッシュ継続回数はラッシュ突入回数約「2.5回」の場合、下限0回、上限8.8回が平均になりえる。
ですので多くの場合は試行回数を増やして、平均値に収束するための「発生率が低いレアケース」を引かない限り、「発生率が高い展開」になります。
ボーダー
次にボーダーで、ボーダーは平均値と中央値で数値が変わります。
| 交換率 | 平均値 | 中央値 | 発生率(高) |
|---|---|---|---|
| 25玉(4.0円) | 17.24 | 21.76 | 22.75 |
| 26玉(3.85円) | 17.93 | 22.63 | 23.66 |
| 27玉(3.70円) | 18.62 | 23.50 | 24.57 |
| 28玉(3.57円) | 19.31 | 24.37 | 25.48 |
| 30玉(3.57円) | 20.69 | 26.11 | 27.30 |
| 33玉(3.03円) | 22.76 | 28.72 | 30.03 |
| 40玉(2.5円) | 27.58 | 34.81 | 36.40 |
※独自計算値
等価交換での「平均」のボーダーは「約17.2」ですが、「中央値」では「約21.7」。
そして今回の「発生率が高い展開」では「約22.7」とかなり高くなります。
目先の勝ち負けであれば、このボーダーに近づかないと厳しい。
ただ最終的に長い目で見れば、平均のボーダーになります。
【おまけ】「平均」パターンの展開
最後におまけで、全てが「平均パターンの展開」だとこんな感じになります。
「平均」数値
- 大当たり回転数:平均「約257.9回」
- ラッシュ継続回数:平均「約3.6回」
- トータル初当たり期待値:平均「約3700個」




貸出&交換率を計算
細かいロスを抜きにすれば結果は差玉ほぼ0個。
合計金額は「約マイナス4,000円」。
軍資金は「約31,000円」でした。
| レート | 項目 | 平均 | 1~10回 | 1~20回 |
|---|---|---|---|---|
| 【交換率】 | 232玉貸し出し | -31029.6 | -62697.0 | -118566.8 |
| 27玉交換(3.70円) | 26638.0 | 24935.2 | 103261.4 | |
| 金額 | -4391.7 | -37761.8 | -15305.4 |
ちなみに貸出は1,000円で232玉、1玉約4.31 円。
交換率は27玉、約3.7円で計算しています
まとめ
今回のテーマ「eルパン三世VSキャッツ・アイ」では、大体こんな展開はいかがでしたか?


- 「発生率が高い展開」で差額は「約マイナス31,000円」
- 軍資金は数日で「約58,000円」
- 「発生率が低いレアな展開」で差額は「約マイナス15,000円」
- 軍資金は数日で「約120,000円」
- 「平均パターンの展開」で差額は「約マイナス4,000円」
- 軍事金は数日で「約31,000円」
このような内容でした。
当たりが軽くてもしっかりした出玉が少なく、軍資金がかさんでいる印象でした。
とくに平均通りの場合と比較すると、波が荒いのが分かります。
軽いからと考えていると軍資金が足りなくなるかもしれませんので、ご注意ください。
備考
関連記事
このサイトが大切にしていること
「この世界は、生きづらいものだ」と思っていた過去があります。
でも今は、そう感じていたのは“思考の回路”が乱れていただけだったんだと気づきました。
このサイト「ゆるやめ」では機械保全士として培った現実重視の“視点”をベースに、脳科学や心理学の知識そして私自身の体験を交えて、我慢ではなく緩やかな仕組みでやめるヒントをお届けしています。
よければ他の記事も覗いてみてくださいね。








